Z-filter MQ-MAS phase cycling
Below are presented some phase cycling procedures for MQ-MAS with three-pulse z-filter
sequence applied to half-integer quadrupole spins:
(1) in amplitude-modulated experiment involving two coherence transfer pathways,
(2) in phase-modulated experiment involving one coherence transfer pathway.
We only consider the usual case where the receiver can take four phases: 0°, 90°, 180°, and 270°.
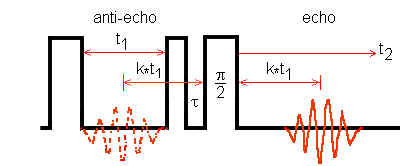
Two approaches are used for the simulation of the echo and/or antiecho amplitudes with
SIMPSON1.1.1 Tcl scripts:
(1) filtering the desired coherences;
(2) explicit phase cycling the pulses and the receiver.
These two approaches are applied to the two practical cases:
(1) the three pulses have strong amplitudes;
(2) the first two pulses have strong amplitudes and the third has a weak amplitude.
When the phase cycling approach generates the same echo and/or antiecho amplitudes as the filtering approach, the phase cycling procedure is valid whatever the nature (strong pulse or not) of the third pulse.
Outline (A) Amplitude-modulated experiment (A.1) Three strong amplitude pulses (A.1.a) ±3Q-MAS for spin I = 3/2 system (1) 24-phase cycling the first and third pulses (2) Simulation (3) Result (4) Discussion (A.1.b) ±3Q-MAS for spin I = 5/2 system (1) 36-phase cycling the first and second pulses (2) Simulation (3) Result (A.1.c) ±5Q-MAS for spin I = 5/2 system (1) 100-phase cycling the first and second pulses (2) Simulation (3) Result (A.2) Two strong amplitude pulses and one soft pulse (A.2.a) ±3Q-MAS for spin I = 3/2 system (A.2.b) ±3Q-MAS for spin I = 5/2 system (1) 24-phase cycling the first and second pulses (2) Simulation (3) Result (4) Comment (A.2.c) ±5Q-MAS for spin I = 5/2 system (1) 40-phase cycling the first and second pulses (2) Simulation (3) Result (4) Comment (B) Phase-modulated experiment (B.1) Three strong amplitude pulses (B.1.a) -3Q-MAS for spin I = 3/2 system (1) 48-phase cycling the first and third pulses (2) 48-phase cycling the first and second pulses (3) Simulation (4) Result (B.1.b) +3Q-MAS for spin I = 5/2 system (1) 48-phase cycling the first and third pulses (2) 48-phase cycling the first and second pulses (3) 72-phase cycling the first and second pulses (4) Simulation (5) Result (B.2) Two strong amplitude pulses and one soft pulse (B.2.a) -3Q-MAS for spin I = 3/2 system (B.2.b) +3Q-MAS for spin I = 5/2 system (1) 48-phase cycling the first and second pulses (2) Simulation (3) Result (C) Conclusion |
(A) Amplitude-modulated experiment
(A.1) Three strong amplitude pulses
In amplitude-modulated experiment, two coherence transfer pathways 0Q -> -3Q -> 0Q -> -1Q and 0Q -> +3Q -> 0Q -> -1Q are selected. The phase cycling is defined with the two coherence transfer pathways. That is, the phase cycling must be identical for the two coherence transfer pathways.

The total pathway phase φpath for the coherence transfer pathway 0Q -> -3Q -> 0Q -> -1Q is
defined by:
φpath = -3*φ1 + 3*φ2 - φ3 + φrec,
that for the coherence transfer pathway 0Q -> +3Q -> 0Q -> -1Q is
defined by:
φpath = +3*φ1 - 3*φ2 - φ3 + φrec,
where
φ1 is the first-pulse phase;
φ2 is the second-pulse phase;
φ3 is the third-pulse phase;
φrec is the receiver phase.
The receiver phase is defined with the condition: φpath = 0. Therefore, we have two equations
for the receiver phase with three parameters:
φrec = +3*φ1 - 3*φ2 + φ3,
φrec = -3*φ1 + 3*φ2 + φ3,
several mathematical solutions are possible, depending on φ1 = 0, φ2 = 0, or φ3 = 0.
(A.1.a) ±3Q-MAS for spin I = 3/2 system
(1) 24-phase cycling the first and third pulses
The simplest phase cycling procedure for spin I = 3/2 is when the receiver phase is
defined with the condition: φ2 = 0; therefore, the two equations for the receiver phase
become:
φrec = +3*φ1 + φ3,
φrec = -3*φ1 + φ3.
The corresponding solution is: φ1 takes six values and φ3 four values.
| φ1 | 0° 60° 120° 180° 240° 300° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X6 {90°}X6 {180°}X6 {270°}X6 |
| φrec | {0° 180°}X3 {90° 270°}X3 {180° 0°}X3 {270° 90°}X3 |
This is a well-known phase-cycling procedure [S. P. Brown, Thesis, 1997].
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the desired coherences (-3Q and 3Q after the first pulse and 0Q after
the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 24-phase cycling |
|---|---|---|
| 1st-pulse | na-filtering-p1 | na-24-cycling-p1 |
| 2nd-pulse | na-filtering-p2 | na-24-cycling-p2 |
| 3rd-pulse | na-filtering-p3 | na-24-cycling-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches (filtering the desired coherences and 24-phase cycling the first and third pulses and the receiver) provide the same simulation data about the echo and antiecho amplitude of a spin I = 3/2 system.
(4) Discussion
It is tempting to apply six-phase cycling on the first pulse, four-phase cycling
on the second pulse, and no phase cycling on the third pulse. In this case,
the echo and the antiecho coherence transfer pathways have opposite receiver phases:
φrec = +3*φ1 -3*φ2,
φrec = -3*φ1 + 3*φ2.
One way to satisfy the same list for the two receiver phases φrec is to only consider phase cycling with 0° and 180° phases for the receiver. As a result, the four-phase cycling for the second pulse becomes a two-phase cycling. In other words, it is a 12 phase-cycling procedure.
| φ1 | 0° 60° 120° 180° 240° 300° |
|---|---|
| φ2 | {0°}X6 {180°}X6 |
| φ3 | 0° |
| φrec | {0° 180°}X3 {180° 0°}X3 |
This 12-phase cycling selects not only the desired coherence transfer pathways
0Q -> ±3Q -> 0Q -> -1Q,
but also the coherence transfer pathways
0Q -> ±3Q -> +2Q -> -1Q and 0Q -> ±3Q -> -2Q -> -1Q,
as shown in the following figure:

We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the desired coherences (-3Q and 3Q after the first pulse,
and 2Q, 0Q, and -2Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 12-phase cycling |
|---|---|---|
| 1st-pulse | na-12-filtering-p1 | na-12-cycling-p1 |
| 2nd-pulse | na-12-filtering-p2 | na-12-cycling-p2 |
| 3rd-pulse | na-12-filtering-p3 | na-12-cycling-p3 |
It is easy to show that the above 12-phase cycling of the first and the second pulses is equivalent to the following 12-phase cycling of the first and the third pulses:
| φ1 | 0° 60° 120° 180° 240° 300° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X6 {180°}X6 |
| φrec | {0° 180°}X3 {180° 0°}X3 |
The same coherence transfer pathways are involved. This 12-phase cycling has been applied by [D. Rovnyak, C. Filip, B. Itin, A. S. Stern, G. Wagner, R. G. Griffin, and J. C. Hoch, J. Magn. Reson. 161, 43-55 (2003)].
A second way to satisfy the same list for the two receiver phases φrec is to apply six-phase cycling on the second pulse as shown below for spin I = 5/2 system.
(A.1.b) ±3Q-MAS for spin I = 5/2 system
The above 24-phase cycling for spin I = 3/2 system is often applied to spin I = 5/2 system in the literature. But [T. Charpentier, Thesis, 1998] proposes another procedure: 36-phase cycling the first and second pulses and the receiver.
(1) 36-phase cycling the first and second pulses
This procedure describes the case where the receiver phase is
defined with the condition: φ3 = 0; therefore, the two equations for the receiver phase
become:
φrec = +3*φ1 - 3*φ2,
φrec = -3*φ1 + 3*φ2.
The corresponding solution is: φ1 and φ2 take six values.
| φ1 | 0° 60° 120° 180° 240° 300° |
|---|---|
| φ2 | {0°}X6 {60°}X6 {120°}X6 {180°}X6 {240°}X6 {300°}X6 |
| φ3 | 0° |
| φrec | {0° 180°}X3 {180° 0°}X3 |
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the desired coherences (-3Q and 3Q after the first pulse and 0Q
after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filt | 24-ph cycl | 36-ph cycl |
|---|---|---|---|
| 1st-pulse | al-filt-p1 | al-24-cycl-p1 | al-36-cycl-p1 |
| 2nd-pulse | al-filt-p2 | al-24-cycl-p2 | al-36-cycl-p2 |
| 3rd-pulse | al-filt-p3 | al-24-cycl-p3 | al-36-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the desired coherences and 36-phase cycling the first and second pulses and the receiver) provide the same simulation data for echo and antiecho amplitude of I = 5/2 system. However, it is not the case for 24-phase cycling the first and third pulses and the receiver as described for I = 3/2 system. The 36-phase cycling is also valid for spin I = 3/2 system. For I = 7/2 system, this 36-phase cycling also allows the coherence transfer pathways 0Q -> ±3Q -> 6Q -> -1Q and 0Q -> ±3Q -> -6Q -> -1Q to be detected.
(A.1.c) ±5Q-MAS for spin I = 5/2 system
(1) 100-phase cycling the first and second pulses
This procedure [T. Charpentier, Thesis, 1998]
describes the case where the receiver phase is
defined with the condition: φ3 = 0; therefore, the two equations for the receiver phase
become:
φrec = +5*φ1 - 5*φ2,
φrec = -5*φ1 + 5*φ2.
The corresponding solution is: φ1 and φ2 take ten values.
| φ1 | 0° 36° 72° 108° 144° 180° 216° 252° 288° 324° |
|---|---|
| φ2 | {0°}X10 {36°}X10 {72°}X10 {108°}X10 {144°}X10 {180°}X10 {216°}X10 {252°}X10 {288°}X10 {324°}X10 |
| φ3 | 0° |
| φrec | {0° 180°}X5 {180° 0°}X5 |
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the desired coherences (-5Q and 5Q after the first pulse and 0Q
after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 100-phase cycling |
|---|---|---|
| 1st-pulse | al-filtering-p1 | al-100-cycling-p1 |
| 2nd-pulse | al-filtering-p2 | al-100-cycling-p2 |
| 3rd-pulse | al-filtering-p3 | al-100-cycling-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the desired coherences and 100-phase cycling the first and second pulses and the receiver) provide the same simulation data for echo and antiecho amplitude of I = 5/2 system.
For half-integer spin I > 3/2, the two approaches (filtering the desired coherences and phase cycling the pulses and the receiver) provide the same simulation data for echo and antiecho amplitude, if phase cycling is applied to the first and second pulses and the receiver, but not to the third pulse. Since most phase cyclings provided in literature involved the third pulse with four phases, they are valid when the third pulse is a selective pulse [P. J. Dirken, S. C. Kohn, M. E. Smith, and E. R. H. van Eck, Chem. Phys. Lett. 266, 568-574 (1997)] [A. Goldbourt and P. K. Madhu, Annu. Rep. NMR Spectrosc. 54, 81-153 (2005)].
(A.2) Two strong amplitude pulses and one soft pulse
When the third pulse is a weak amplitude pulse, the phase of the second pulse is always zero and four phases are applied to the third pulse.
(A.2.a) ±3Q-MAS for spin I = 3/2 system
The data in the section dealing with ±3Q-MAS for spin I = 3/2 system in the three strong amplitude pulses are applicable to the soft pulse case.
(A.2.b) ±3Q-MAS for spin I = 5/2 system
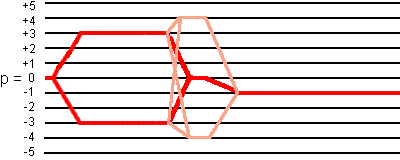
(1) 24-phase cycling the first and third pulses
The 24-phase cycling presented in the section dealing with ±3Q-MAS for spin I = 3/2 system in the three strong amplitude pulses is applied to the soft pulse case.
This 24-phase cycling selects not only the desired coherence transfer pathways
0Q -> ±3Q -> 0Q -> -1Q,
but also the coherence transfer pathways
0Q -> ±3Q -> +4Q -> -1Q and 0Q -> ±3Q -> -4Q -> -1Q
as shown in the following figure:
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (-3Q and 3Q after the first pulse, and 4Q,
0Q, and -4Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 24-phase cycling |
|---|---|---|
| 1st-pulse | al-select-filt-p1 | al-select-24-cycl-p1 |
| 2nd-pulse | al-select-filt-p2 | al-select-24-cycl-p2 |
| 3rd-pulse | al-select-filt-p3 | al-select-24-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 24-phase cycling the first and third pulses and the receiver) provide the same simulation data for echo and antiecho amplitude of I = 5/2 system.
(4) Comment
Sometimes, 12-phase and 24-phase cycling of the second and the third pulses are also applied.
(A.2.c) ±5Q-MAS for spin I = 5/2 system
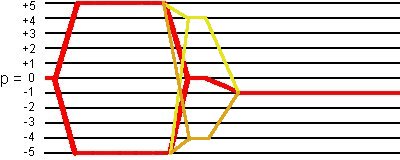
(1) 40-phase cycling the first and third pulses
The following 40-phase cycling is applied:
| φ1 | 0° 36° 72° 108° 144° 180° 216° 252° 288° 324° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X10 {90°}X10 {180°}X10 {270°}X10 |
| φrec | {0° 180°}X5 {90° 270°}X5 {180° 0°}X5 {270° 90°}X5 |
This 40-phase cycling selects not only the desired coherence transfer pathways
0Q -> ±5Q -> 0Q -> -1Q,
but also the coherence transfer pathways
0Q -> ±5Q -> +4Q -> -1Q and 0Q -> ±5Q -> -4Q -> -1Q
as shown in the following figure:
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (-5Q and 5Q after the first pulse,
and 0Q, 4Q, and -4Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 40-phase cycling |
|---|---|---|
| 1st-pulse | al-select-filt-p1 | al-select-40-cycl-p1 |
| 2nd-pulse | al-select-filt-p2 | al-select-40-cycl-p2 |
| 3rd-pulse | al-select-filt-p3 | al-select-40-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 40-phase cycling the first and third pulses and the receiver) provide the same simulation data for echo and antiecho amplitude of I = 5/2 system.
(4) Comment
Sometimes, 40-phase cycling of the second and the third pulses is also applied.
(B) Phase-modulated experiment
(B.1) Three strong amplitude pulses
In some 2D experiments such as the double resonance MQ-HETCOR experiment, one coherence transfer pathway is required. For spin I = 3/2 system, the coherence transfer pathway 0Q -> -3Q -> 0Q -> -1Q is needed. For spin I = 5/2 and 7/2 systems, the coherence transfer pathway 0Q -> +3Q -> 0Q -> -1Q is needed.
In phase-modulated experiment, phase cycling is defined with the desired coherence transfer pathway.
(B.1.a) -3Q-MAS for spin I = 3/2 system
The total pathway phase φpath for the coherence transfer pathway 0Q -> -3Q -> 0Q -> -1Q
is defined by:
φpath = -3*φ1 + 3*φ2 - φ3 + φrec.
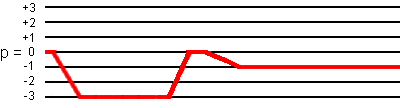
Two 48-phase cycling procedures are possible: one cycling the first and third pulses and one cycling the first and second pulses. Both are valid.
(1) 48-phase cycling the first and third pulses
The receiver phase is defined with the conditions: φpath = 0 and φ2 = 0;
therefore φrec = 3*φ1 + φ3.
To select the desired coherence transfer pathway, φ1 takes 12 values;
φ3 takes four values.
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X12 {90°}X12 {180°}X12 {270°}X12 |
| φrec | {0° 90° 180° 270°}X3 {90° 180° 270° 0°}X3 {180° 270° 0° 90°}X3 {270° 0° 90° 180°}X3 |
(2) 48-phase cycling the first and second pulses
The receiver phase is defined with the conditions: φpath = 0 and φ3 = 0:
therefore φrec = 3*φ1 - 3*φ2.
To select the desired coherence transfer pathway, φ1 takes 12 values;
φ2 takes four values.
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | {0°}X12 {90°}X12 {180°}X12 {270°}X12 |
| φ3 | 0° |
| φrec | {0° 90° 180° 270°}X3 {90° 180° 270° 0°}X3 {180° 270° 0° 90°}X3 {270° 0° 90° 180°}X3 |
The above two 48-phase cycling procedures have the same receiver phase.
(3) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo amplitude versus a
pulse duration with two approaches:
(a) filtering the desired coherence (-3Q after the first pulse and 0Q after the
second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 48-cycling p1 p3 |
48-cycling p1 p2 |
|---|---|---|---|
| 1st-pulse | na-filt-p1 | na-p1p3-p1 | na-p1p2-p1 |
| 2nd-pulse | na-filt-p2 | na-p1p3-p2 | na-p1p2-p2 |
| 3rd-pulse | na-filt-p3 | na-p1p3-p3 | na-p1p2-p3 |
(4) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about the echo amplitude of spin I = 3/2 system.
(B.1.b) +3Q-MAS for spin I = 5/2 system
The total pathway phase φpath for the coherence transfer pathway 0Q -> +3Q -> 0Q -> -1Q
is defined by:
φpath = 3*φ1 - 3*φ2 - φ3 + φrec.
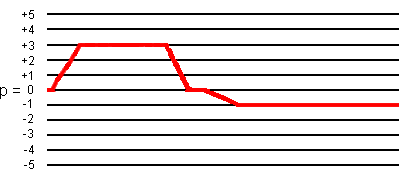
Several phase cycling procedures are possible. But only one is valid.
(1) 48-phase cycling the first and third pulses
The receiver phase is defined with the following conditions: φpath = 0 and φ2 = 0;
therefore φrec = -3*φ1 + φ3.
To select the desired coherence transfer pathway, φ1 takes 12 values;
φ3 takes four values.
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X12 {90°}X12 {180°}X12 {270°}X12 |
| φrec | {0° 270° 180° 90°}X3 {90° 0° 270° 180°}X3 {180° 90° 0° 270°}X3 {270° 180° 90° 0°}X3 |
(2) 48-phase cycling the first and second pulses
The receiver phase is defined with the following conditions: φpath = 0 and φ3 = 0;
therefore φrec = -3*φ1 + 3*φ2.
To select the desired coherence transfer pathway, φ1 takes 12 values;
φ2 takes four values.
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | {0°}X12 {90°}X12 {180°}X12 {270°}X12 |
| φ3 | 0° |
| φrec | {0° 90° 180° 270°}X3 {90° 180° 270° 0°}X3 {180° 270° 0° 90°}X3 {270° 0° 90° 180°}X3 |
The above two 48-phase cycling procedures have different receiver phase.
(3) 72-phase cycling the first and second pulses
The receiver phase is defined with the following conditions: φpath = 0 and φ3 = 0;
therefore φrec = -3*φ1 + 3*φ2.
To select the desired coherence transfer pathway, φ1 takes 12 values;
φ2 takes six values.
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | {0°}X12 {60°}X12 {120°}X12 {180°}X12 {240°}X12 {300°}X12 |
| φ3 | 0° |
| φrec | {0° 270° 180° 90°}X3 {180° 90° 0° 270°}X3 |
(4) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo amplitude versus a
pulse duration with two approaches:
(a) filtering the desired coherences (+3Q after the first pulse and 0Q
after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 48-cycling p1 p3 |
48-cycling p1 p2 |
|---|---|---|---|
| 1st-pulse | al-filt-p1 | al-p1p3-p1 | al-p1p2-p1 |
| 2nd-pulse | al-filt-p2 | al-p1p3-p2 | al-p1p2-p2 |
| 3rd-pulse | al-filt-p3 | al-p1p3-p3 | al-p1p2-p3 |
| Duration | Filtering | 72-cycling p1 p2 |
|---|---|---|
| 1st-pulse | al-72-filt-p1 | al-72-p1p2-p1 |
| 2nd-pulse | al-72-filt-p2 | al-72-p1p2-p2 |
| 3rd-pulse | al-72-filt-p3 | al-72-p1p2-p3 |
(5) Result
The two 48-phase cycling procedures, applied to spin I = 5/2 system, generate echo amplitudes different of those generated by the filtering approach.
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the desired coherences and 72-phase cycling the first and second pulses and the receiver) provide the same simulation data about the echo amplitude of spin I = 5/2 system.
(B.2) Two strong amplitude pulses and one soft pulse
(B.2.a) -3Q-MAS for spin I = 3/2 system
The data in the section dealing with -3Q-MAS for spin I = 3/2 system in the three strong amplitude pulses are applicable to the soft pulse case.
(B.2.b) +3Q-MAS for spin I = 5/2 system
(1) 48-phase cycling the first and third pulses
The following 48-phase cycling is applied:
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X12 {90°}X12 {180°}X12 {270°}X12 |
| φrec | {0° 270° 180° 90°}X3 {90° 0° 270° 180°}X3 {180° 90° 0° 270°}X3 {270° 180° 90° 0°}X3 |
This 48-phase cycling selects not only the desired coherence transfer pathways
0Q -> +3Q -> 0Q -> -1Q,
but also the coherence transfer pathways
0Q -> +3Q -> -4Q -> -1Q and 0Q -> +3Q -> +4Q -> -1Q
as shown in the following figure:
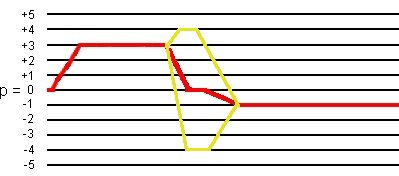
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo amplitude versus a
pulse duration with two approaches:
(a) filtering the coherences (+3Q after the first pulse,
and 0Q, -4Q, and 4Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 48-cycling p1 p3 |
|---|---|---|
| 1st-pulse | al-select-filt-p1 | al-select-p1p3-cycl-p1 |
| 2nd-pulse | al-select-filt-p2 | al-select-p1p3-cycl-p2 |
| 3rd-pulse | al-select-filt-p3 | al-select-p1p3-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 48-phase cycling the first and third pulses and the receiver) provide the same simulation data about the echo amplitude of spin I = 5/2 system.
(C) Conclusion
For three-pulse z-filtered MQ-MAS sequences, filtering the desired coherences and phase cycling the pulses and the receiver may not generate the same simulation data for echo and/or antiecho amplitude, depending on the experiment.
When a phase cycling approach generates the same echo and/or antiecho amplitudes as the filtering approach, the phase cycling procedure is valid whatever the nature (strong amplitude pulse or not) of the third pulse.
When the amplitude of the third pulse has a significant effect on the signal-to-noise ratio, the choice of the phase cycling becomes an important acquisition parameter.
