12-phase and 24-phase cycling of the second and the third pulses in 3-pulse z-filter ±3Q-MAS of I = 5/2
[an error occurred while processing this directive]Z-filter MQ-MAS with 12-phase cycling
Two approaches:
(1) filtering the coherences,
(2) explicit phase cycling the pulses and the receiver,
are used for the simulation of echo and antiecho amplitude in
±3Q-MAS of spin I = 5/2 system. The sequence consists of two
strong amplitude pulses followed by a weak amplitude pulse.
(1) 12-phase cycling the second and the third pulses
Sometimes, the following phase cycling [G. Wu and S. Dong, J. Am. Chem. Soc. 123, 9119-9125 (2001)] is used:
| φ1 = | 0° |
|---|---|
| φ2 = | 0° 60° 120° 180° 240° 300° |
| φ3 = | {0°}X6 {180°}X6 |
| φrec = | {0° 180°}X3 {180° 0°}X3 |
This 12-phase cycling selects the three families of coherence transfer pathways:
- 0Q -> (+5Q, -1Q) -> (+2Q, -4Q) -> -1Q,
- 0Q -> (+1Q, -5Q) -> (+4Q, -2Q) -> -1Q,
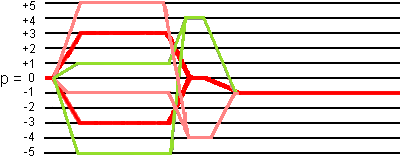
- 0Q -> ±3Q -> 0Q -> -1Q (the desired coherence transfer pathways),
as shown in the following figure. Family a is pink pathways, family b is green pathways, and family c is red pathways:
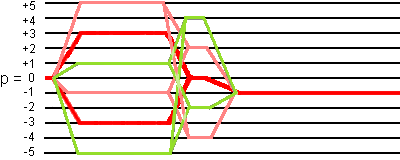
These three families have common coherence transfer pathways only before the the three pulses (0Q coherence) and during the detection (-1Q coherence). Otherwise, they are independent.
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration:
(1) filtering the coherences (a Tcl script is associated with each family),
(2) 12-phase cycling the pulses and the receiver.
| Duration | Filtering | 12-phase cycling |
|---|---|---|
| 1st-pulse | al-p2p3-cycl-p1 | |
| 2nd-pulse | al-p2p3-cycl-p2 | |
| 3rd-pulse | al-p2p3-cycl-p3 |
(3) Result
The simulation parameters are defined in the Tcl scripts. The below three figures represent the variations of the echo and antiecho amplitude versus a pulse duration for the three families of coherence transfer pathways (a, b, and c). The blue curve or a+b+c curve is their sum. The variation of echo and antiecho amplitude provided by the 12-phase cycling procedure is represented by red squares.
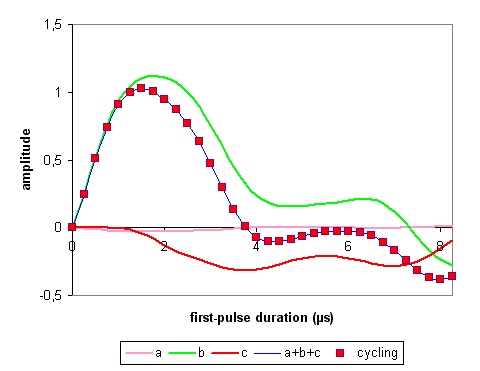
The first-pulse duration that maximizes the a+b+c curve depends on the durations of the other two pulses.
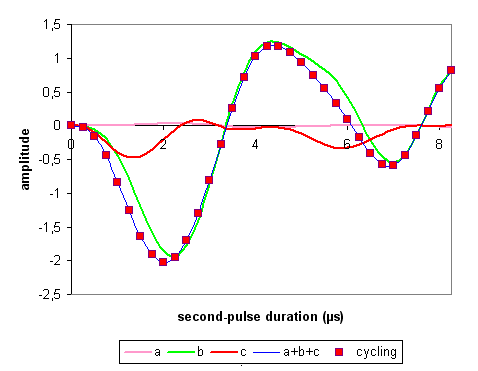
The second-pulse duration that maximizes the a+b+c curve depends on the durations of the other two pulses.
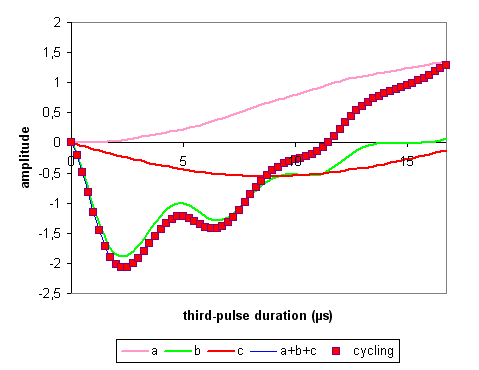
The third-pulse duration that maximizes the a+b+c curve depends on the durations of the other two pulses.
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 12-phase cycling the second and third pulses and the receiver) provide the same simulation data for echo and antiecho amplitude of I = 5/2 system. In our simulation condtions, the main contribution to the echo and antiecho amplitude is provided by family b, that is the coherence transfer pathways 0Q -> (+1Q, -5Q) -> (+4Q, -2Q) -> -1Q, instead of the desired coherence transfer pathways, family c or 0Q -> ±3Q -> 0Q -> -1Q.
Since three independent families contribute to the echo and antiecho amplitude, the durations of the three pulses that maximize this amplitude are not unique.
We also provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho amplitude (a+b+c curve) versus a pulse duration by the coherence filtering method:
| Duration | Filtering |
|---|---|
| 1st-pulse | al-12p2p3-filtering-p1 |
| 2nd-pulse | al-12p2p3-filtering-p2 |
| 3rd-pulse | al-12p2p3-filtering-p3 |
Z-filter MQ-MAS with 24-phase cycling
(1) 24-phase cycling the second and the third pulses
G. Wu [in Modern Magnetic Resonance, Graham A. Webb (Ed), Springer, Dordrecht, pages 691-697 (2006)] also suggests a 24-phase cycling procedure.
| φ1 = | 0° |
|---|---|
| φ2 = | 0° 60° 120° 180° 240° 300° |
| φ3 = | {0°}X6 {90°}X6 {180°}X6 {270°}X6 |
| φrec = | {0° 180°}X3 {90° 270°}X3 {180° 0°}X3 {270° 90°}X3 |
The following coherence transfer pathways are involved:
(2) Simulation
We provide SIMPSON2 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration:
(1) filtering the coherences (a Tcl script is associated with each family),
(2) 24-phase cycling the pulses and the receiver.
| Duration | Filtering | 24-phase cycling |
|---|---|---|
| 1st-pulse |
a + b + c: total-p1 |
al-p2p3-cycl-p1 |
| 2nd-pulse |
a + b + c: total-p2 |
al-p2p3-cycl-p2 |
| 3rd-pulse |
a + b + c: total-p3 |
al-p2p3-cycl-p3 |
(top)