Shifted-echo MQ-MAS phase cycling
Below are presented phase cycling procedures [D. Massiot, B. Touzo,
D. Trumeau, J. P. Coutures, J. Virlet, P. Florian, and P. J. Grandinetti,
Solid State NMR 6, 73-83 (1996)] for MQ-MAS with shifted-echo sequence
applied to half-integer quadrupole spins:
(1) in amplitude-modulated experiment involving two coherence transfer pathways,
(2) in phase-modulated experiment involving one coherence transfer pathway.
We only consider the usual case where the receiver can take four phases: 0°, 90°, 180°, and 270°.
Two approaches are used for the simulation of the echo and/or antiecho
amplitudes with SIMPSON1.1.1 Tcl scripts:
(1) filtering the desired coherences;
(2) explicit phase cycling the pulses and the receiver.
These two approaches are applied to the two practical cases:
(1) the three pulses have strong amplitudes;
(2) the first two pulses have strong amplitudes and the third has a weak amplitude.
For three-pulse sequences such as shifted-echo 3Q-MAS experiments, these two approaches provide the same simulation data about echo and/or antiecho amplitudes whatever the nature (strong or not) of the third pulse.
Outline (A) Amplitude-modulated experiment (A.1) Three strong amplitude pulses (A.1.a) ±3Q-MAS for spin I = 3/2 system (1) 48-phase cycling (2) Simulation (3) Result (A.1.b) ±5Q-MAS for spin I = 5/2 system (1) 80-phase cycling (2) Simulation (3) Result (A.2) Two strong amplitude pulses and one soft pulse (A.2.a) ±3Q-MAS for spin I = 3/2 system (1) 24-phase cycling (2) Simulation (3) Result (A.2.b) ±3Q-MAS for spin I = 5/2 system (1) 24-phase cycling (2) Simulation (3) Result (A.2.c) ±5Q-MAS for spin I = 5/2 system (1) 40-phase cycling (2) Simulation (3) Result (B) Phase-modulated experiment (B.1) Three strong amplitude pulses (B.1.a) -3Q-MAS for spin I = 3/2 system (1) 96-phase cycling (2) Simulation (3) Result (B.1.b) +3Q-MAS for spin I = 3/2 system (1) 96-phase cycling (2) Simulation (3) Result (B.2) Two strong amplitude pulses and one soft pulse (B.2.a) -3Q-MAS for spin I = 3/2 system (1) 48-phase cycling (2) Simulation (3) Result (B.2.b) +3Q-MAS for spin I = 3/2 system (1) 48-phase cycling (2) Simulation (3) Result (C) Conclusion |
(A) Amplitude-modulated experiment
(A.1) Three strong amplitude pulses
The pulse sequence consists of three strong amplitude pulses.
(A.1.a) ±3Q-MAS for spin I = 3/2 system
In amplitude-modulated experiment, two coherence transfer pathways 0Q -> -3Q -> +1Q -> -1Q and 0Q -> +3Q -> +1Q ->-1Q are selected. The phase cycling is defined with the two coherence transfer pathways. That is, the phase cycling must be identical for the two coherence transfer pathways.
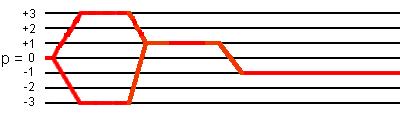
The total pathway phase φpath for the coherence transfer pathway
0Q -> -3Q -> +1Q -> -1Q is defined by:
φpath = -3*φ1 + 4*φ2 - 2*φ3 + φrec,
that for the coherence transfer pathway 0Q -> +3Q -> +1Q -> -1Q is defined by:
φpath = +3*φ1 - 2*φ2 - 2*φ3 + φrec,
where
φ1 is the first-pulse phase;
φ2 is the second-pulse phase;
φ3 is the third-pulse phase;
φrec is the receiver phase.
(1) 48-phase cycling
The receiver phase is defined with the conditions: φpath = 0
and φ2 = 0. Therefore, we have two equations
for the receiver phase with two parameters:
φrec = +3*φ1 + 2*φ3,
φrec = -3*φ1 + 2*φ3.
The corresponding solution is: φ1 takes six values; φ3 takes eight values.
| φ1 | 0° 60° 120° 180° 240° 300° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X6 {45°}X6 {90°}X6 {135°}X6 {180°}X6 {225°}X6 {270°}X6 {315°}X6 |
| φrec | {0° 180°}X3 {90° 270°}X3 {180° 0°}X3 {270° 90°}X3 |
This phase cycling procedure is also used by [Vosegaard and coworkers, Multiple quantum magic-angle-spinning using rotary resonance excitation, J. Chem. Phys. 114, 4618-4624 (2001)].
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(1) filtering the desired coherences (-3Q and 3Q after the first pulse and
+1Q after the second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 48-phase cycling |
|---|---|---|
| 1st-pulse | na-filtering-p1 | na-48-cycling-p1 |
| 2nd-pulse | na-filtering-p2 | na-48-cycling-p2 |
| 3rd-pulse | na-filtering-p3 | na-48-cycling-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about echo and antiecho amplitude for spin I = 3/2 and 5/2 systems. For spin I = 7/2 systems, this 48-phase cycling also allows the coherence transfer pathways 0Q -> ±3Q -> -7Q -> -1Q to be detected.
(A.1.b) ±5Q-MAS for spin I = 5/2 system
(1) 80-phase cycling
The receiver phase is defined with the conditions: φpath = 0
and φ2 = 0. Therefore, we have two equations
for the receiver phase with two parameters:
φrec = +5*φ1 + 2*φ3,
φrec = -5*φ1 + 2*φ3.
The corresponding solution is: φ1 takes ten values; φ3 takes eight values.
| φ1 | 0° 36° 72° 108° 144° 180° 216° 252° 288° 324° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X10 {45°}X10 {90°}X10 {135°}X10 {180°}X10 {225°}X10 {270°}X10 {315°}X10 |
| φrec | {0° 180°}X5 {90° 270°}X5 {180° 0°}X5 {270° 90°}X5 |
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(1) filtering the desired coherences (-5Q and 5Q after the first pulse and
+1Q after the second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 80-phase cycling |
|---|---|---|
| 1st-pulse | al-filtering-p1 | al-80-cycling-p1 |
| 2nd-pulse | al-filtering-p2 | al-80-cycling-p2 |
| 3rd-pulse | al-filtering-p3 | al-80-cycling-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about echo and antiecho amplitude for spin I = 5/2 systems. For spin I = 7/2 systems, this 80-phase cycling also allows the coherence transfer pathways 0Q -> ±5Q -> -7Q -> -1Q to be detected.
(A.2) Two strong amplitude pulses and one soft pulse
The first two pulses of the sequence have strong amplitudes whereas the third pulse has a weak amplitude.
(A.2.a) ±3Q-MAS for spin I = 3/2 system
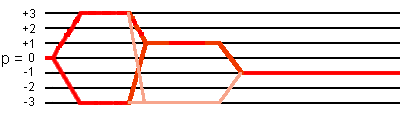
When the third pulse has a weak amplitude, a four-phase cycling is applied to this pulse instead of eight-phase cycling in the strong amplitude case. As a result, the number of phase cycling reduces to 24.
(1) 24-phase cycling
The following phase cycling is applied:
| φ1 | 0° 60° 120° 180° 240° 300° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X6 {90°}X6 {180°}X6 {270°}X6 |
| φrec | {0° 180°}X3 {180° 0°}X3 |
This 24-phase cycling selects not only the desired coherence transfer pathways
0Q -> ±3Q -> +1Q -> -1Q,
but also the coherence transfer pathways
0Q -> ±3Q -> -3Q -> -1Q,
as shown in the following figure:
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(1) filtering the coherences (-3Q and 3Q after the first pulse, and
+1Q and -3Q after the second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 24-phase cycling |
|---|---|---|
| 1st-pulse | na-select-filt-p1 | na-select-24-cycl-p1 |
| 2nd-pulse | na-select-filt-p2 | na-select-24-cycl-p2 |
| 3rd-pulse | na-select-filt-p3 | na-select-24-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about echo and antiecho amplitude for spin I = 3/2 systems.
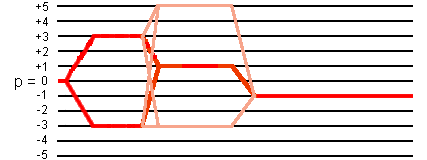
(A.2.b) ±3Q-MAS for spin I = 5/2 system
The above 24-phase cycling is also applicable to spin I = 5/2 systems.
(1) 24-phase cycling
This 24-phase cycling selects not only the desired coherence transfer pathways
0Q -> ±3Q -> +1Q -> -1Q,
but also the coherence transfer pathways
0Q -> ±3Q -> -3Q -> -1Q and 0Q -> ±3Q -> +5Q -> -1Q
as shown in the following figure:
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(1) filtering the coherences (-3Q and 3Q after the first pulse, and
+1Q, +5Q, and -3Q after the second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 24-phase cycling |
|---|---|---|
| 1st-pulse | al-select-filt-p1 | al-select-24-cycl-p1 |
| 2nd-pulse | al-select-filt-p2 | al-select-24-cycl-p2 |
| 3rd-pulse | al-select-filt-p3 | al-select-24-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about echo and antiecho amplitude for spin I = 5/2 systems.
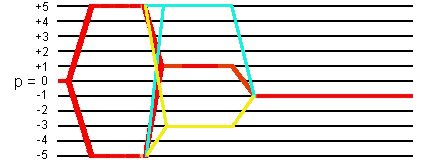
(A.2.c) ±5Q-MAS for spin I = 5/2 system
(1) 40-phase cycling
Since four-phase cycling is applied to the weak amplitude pulse, the following 40-phase cycling is applied:
| φ1 | 0° 36° 72° 108° 144° 180° 216° 252° 288° 324° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X10 {90°}X10 {180°}X10 {270°}X10 |
| φrec | {0° 180°}X5 {180° 0°}X5 |
This 40-phase cycling selects not only the desired coherence transfer pathways
0Q -> ±5Q -> +1Q -> -1Q,
but also the coherence transfer pathways
0Q -> ±5Q -> -3Q -> -1Q and 0Q -> ±5Q -> +5Q -> -1Q ,
as shown in the following figure:
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo and antiecho
amplitude versus a pulse duration with two approaches:
(1) filtering the coherences (-5Q and 5Q after the first pulse, and
+1Q, -3Q, and 5Q after the second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 40-phase cycling |
|---|---|---|
| 1st-pulse | al-select-filt-p1 | al-select-40-cycl-p1 |
| 2nd-pulse | al-select-filt-p2 | al-select-40-cycl-p2 |
| 3rd-pulse | al-select-filt-p3 | al-select-40-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about echo and antiecho amplitude for spin I = 5/2 systems.
(B) Phase-modulated experiment
(B.1) Three strong amplitude pulses
In phase-modulated experiment, phase cycling is defined with the desired coherence transfer pathway. Since the coherence transfer pathways are identical to those involved in split-t1 experiments, these phase cycling procedures are applicable for both experiments.
(B.1.a) -3Q-MAS for spin I = 3/2 system
We discuss the echo coherence transfer pathway for a spin I = 3/2 system.
(1) 96-phase cycling
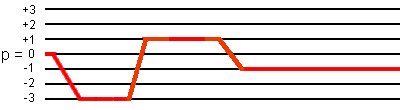
The total pathway phase φpath for the coherence transfer pathway
0Q -> -3Q -> +1Q -> -1Q is defined by:
φpath = -3*φ1 + 4*φ2 - 2*φ3 + φrec.
The receiver phase is defined with the conditions: φpath = 0 and φ2 = 0 ;
therefore φrec = 3*φ1 + 2*φ3.
φ1 takes 12 values;
φ3 takes eight values.
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X12 {45°}X12 {90°}X12 {135°}X12 {180°}X12 {225°}X12 {270°}X12 {315°}X12 |
| φrec | {0° 90° 180° 270°}X3 {90° 180° 270° 0°}X3 {180° 270° 0° 90°}X3 {270° 0° 90° 180°}X3 |
This phase cycling procedure is also provided by [S. P. Brown and S. Wimperis Two-dimensional MQ-MAS NMR of quadrupolar nuclei: a comparison of methods, J. Magn. Reson. 128, 42-61 (1997)].
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo amplitude versus a
pulse duration with two approaches:
(1) filtering the desired coherences (-3Q after the first pulse and +1Q after the
second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 96-phase cycling |
|---|---|---|
| 1st-pulse | na-echo-filt-p1 | na-echo-96-cycl-p1 |
| 2nd-pulse | na-echo-filt-p2 | na-echo-96-cycl-p2 |
| 3rd-pulse | na-echo-filt-p3 | na-echo-96-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about echo amplitude for spin I = 3/2 and about antiecho amplitude for spin I = 5/2 systems. For spin I = 7/2 systems, this 96-phase cycling also allows the coherence transfer pathway 0Q -> -3Q -> -7Q -> -1Q to be detected.
(B.1.b) +3Q-MAS for spin I = 3/2 system
We discuss the antiecho coherence transfer pathway for a spin I = 3/2 system.
(1) 96-phase cycling
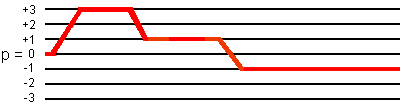
The total pathway phase φpath for the coherence transfer pathway
0Q -> +3Q -> +1Q -> -1Q is defined by:
φpath = 3*φ1 - 2*φ2 - 2*φ3 + φrec.
The receiver phase is defined with the conditions: φpath = 0 and φ2 = 0;
therefore φrec = -3*φ1 + 2*φ3.
φ1 takes 12 values;
φ3 takes eight values.
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X12 {45°}X12 {90°}X12 {135°}X12 {180°}X12 {225°}X12 {270°}X12 {315°}X12 |
| φrec | {0° 270° 180° 90°}X3 {90° 0° 270° 180°}X3 {180° 90° 0° 270°}X3 {270° 180° 90° 0°}X3 |
This phase cycling procedure is also provided by [S. P. Brown and S. Wimperis Two-dimensional MQ-MAS NMR of quadrupolar nuclei: a comparison of methods, J. Magn. Reson. 128, 42-61 (1997)].
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the antiecho amplitude versus a
pulse duration with two approaches:
(1) filtering the desired coherences (+3Q after the first pulse and +1Q after the
second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 96-phase cycling |
|---|---|---|
| 1st-pulse | na-anti-filt-p1 | na-anti-96-cycl-p1 |
| 2nd-pulse | na-anti-filt-p2 | na-anti-96-cycl-p2 |
| 3rd-pulse | na-anti-filt-p3 | na-anti-96-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation date about antiecho amplitude for spin I = 3/2 systems and about echo amplitude for spin I = 5/2 systems. For spin I = 7/2 systems, this 96-phase cycling also allows the coherence transfer pathway 0Q -> +3Q -> -7Q -> -1Q to be detected.
(B.2) Two strong amplitude pulses and one soft pulse
The first two pulses of the sequence have strong amplitudes whereas the third pulse has a weak amplitude.
(B.2.a) -3Q-MAS for spin I = 3/2 system
When the third pulse has a weak amplitude, a four-phase cycling is applied to this pulse instead of eight-phase cycling in the strong amplitude case. As a result, the number of phase cycling reduces to 48.
(1) 48-phase cycling
The following phase cycling is applied:
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X12 {90°}X12 {180°}X12 {270°}X12 |
| φrec | {0° 90° 180° 270°}X3 {180° 270° 0° 90°}X3 |
This 48-phase cycling selects not only the desired coherence transfer pathway
0Q -> -3Q -> +1Q -> -1Q,
but also the coherence transfer pathway
0Q -> -3Q -> -3Q -> -1Q,
as shown in the following figure:
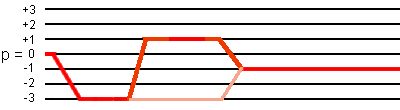
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo amplitude versus a
pulse duration with two approaches:
(1) filtering the coherences (-3Q after the first pulse, and +1Q and -3Q after the
second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 48-phase cycling |
|---|---|---|
| 1st-pulse | na-echo-sel-filt-p1 | na-echo-sel-cycl-p1 |
| 2nd-pulse | na-echo-sel-filt-p2 | na-echo-sel-cycl-p2 |
| 3rd-pulse | na-echo-sel-filt-p3 | na-echo-sel-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation data about echo amplitude for spin I = 3/2 systems.
(B.2.b) +3Q-MAS for spin I = 3/2 system
We discuss the antiecho coherence transfer pathway for a spin I = 3/2 system.
(1) 48-phase cycling
The following 48-phase cycling is applied:
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | {0°}X12 {90°}X12 {180°}X12 {270°}X12 |
| φrec | {0° 270° 180° 90°}X3 {180° 90° 0° 270°}X3 |
This 48-phase cycling selects not only the desired coherence transfer pathway
0Q -> +3Q -> +1Q -> -1Q,
but also the coherence transfer pathway
0Q -> +3Q -> -3Q -> -1Q,
as shown in the following figure:
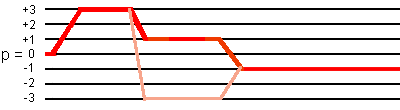
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the antiecho amplitude versus a
pulse duration with two approaches:
(1) filtering the coherences (+3Q after the first pulse, and +1Q and -3Q after the
second pulse);
(2) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 48-phase cycling |
|---|---|---|
| 1st-pulse | na-anti-sel-filt-p1 | na-anti-sel-48-cycl-p1 |
| 2nd-pulse | na-anti-sel-filt-p2 | na-anti-sel-48-cycl-p2 |
| 3rd-pulse | na-anti-sel-filt-p3 | na-anti-sel-48-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same simulation date about antiecho amplitude for spin I = 3/2.
(C) Conclusion
In shifted-echo experiments for I = 3/2 and 5/2 systems, two cases are presented:
- the three pulses have strong amplitudes - the desired coherence transfer pathways are selected by phase cycling;
- the first two pulses have strong amplitudes and the third pulse has a weak amplitude - not only the desired coherence transfer pathways are selected, but additional coherence transfer pathways are also selected by phase cycling.
In the two cases, the variation of the echo and/or antiecho amplitudes versus a pulse duration can be simulated with coherence filtering method and phase cycling method. But the coherence filtering method provides the results in much shorter time.
