FAst Spinning gives Transfer Enhancement at Rotary resonance MQ-MAS

Vosegaard and coworkers discovered the FASTER MQMAS method which increases the sensitivity of MQMAS experiment in the sudden passage regime, that is,

1. omegaRF*omegaRF/(omegaQ*omegaROT) « 1 ,
2. in practice, applying low RF pulses and using high rotor spinning speed.

The RF field strength is omegaRF and the MAS frequency of the rotor is omegaROT.

The sensitivity of triple-quantum preparation and mixing in MQ-MAS experiment is enhanced by the rotary resonance between omegaRF and omegaROT. The rotary resonance effects are observed when omegaRF is a multiple of omegaROT.

For I = 3/2, Vosegaard and coworkers reported that:

(1) The triple-quantum coherence is created from the triple-quantum z-magnetization when

(n - 1)*omegaROT < 2*omegaRF < n*omegaROT

with minimum efficiency occurring at 2*omegaRF = n*omegaROT.

(2) The triple-quantum coherence is efficiently transferred to the central transition coherence at rotary resonance, omegaRF = n*omegaROT.

For I = 5/2, Walls and coworkers reported that:

(1) The 5Q and 3Q coherences are created from the z-magnetization via a nutation mechanism when

2*n *omegaROT < 3*omegaRF < 2*(n + 1)*omegaROT.

Furthermore, effective transfer occurs between 5Q and 3Q coherences.

(2) Both 5Q and 3Q coherences are efficiently transferred to the central transition coherence at rotary resonance, omegaRF = 2*n*omegaROT/3.

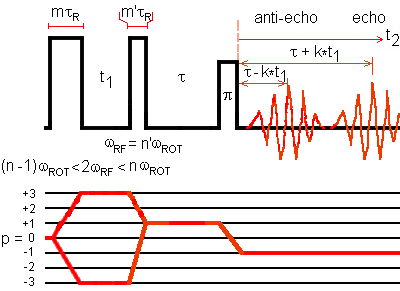
This figure represents FASTER 3QMAS experiment using the amplitude modulated shifted-echo approach.

The delay tau should be long enough so that the whole echo is acquired for t1 = 0. This delay is a multiple of the rotor period and about half the echo width.

ACQUISITION: Hypercomplex or TPPI

PROCESSING: After the Fourier transform with respect to t2, a tau-dependent first-order phase correction is performed to remove the phase modulation due to the shift and a t1-dependent first-order phase correction to perform the shearing transformation. This results a 2D isotropic (in F1 dimension) anisotropic (in the F2 dimension) correlation spectrum.