SPAM MQ-MAS phase cycling
Below are presented some phase cycling procedures for SPAM MQ-MAS sequence applied to quadrupole spins I = 3/2 and 5/2.
We only consider the usual case where the receiver can take four phases: 0°, 90°, 180°, and 270°.
The first two pulses have strong amplitudes but the third pulse has a weak amplitude. We deal with the echo/antiecho acquisition of SPAM presented by Amoureux and coworkers.
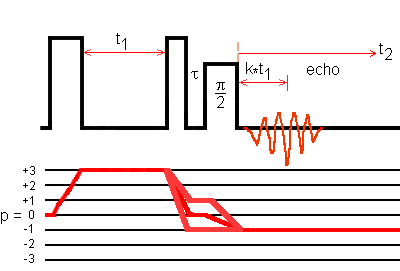
Fig. 1: Ideal SPAM 3Q-MAS echo transfer pathways for a spin I = 5/2 system. The second and third pulses are X-pulses.
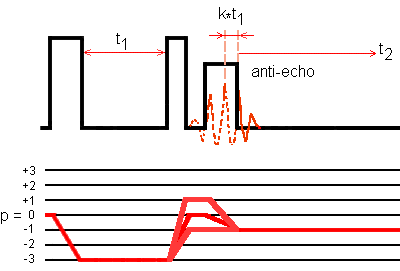
Fig. 2: Ideal SPAM -3Q-MAS antiecho transfer pathways for a spin I = 5/2 system. The second pulse is an X-pulse and the third pulse is a -X-pulse.
Two approaches are used for the simulation of the echo or antiecho amplitudes with
SIMPSON1.1.1 Tcl scripts:
(1) filtering the coherences;
(2) explicit phase cycling the first pulse and the receiver.
In fact, more coherences have to be taken into account during the evolution period between the second and the third pulses. When the amplitudes are normalized to the number of phase cycling, these two approaches provide the same echo or antiecho amplitudes.
Outline (A) Spin I = 3/2 system (A.1) -3Q echo (1) 12-phase cycling the first pulse and the receiver (2) Simulation (3) Result (A.2) +3Q antiecho (1) 12-phase cycling the first and the receiver (2) Simulation (3) Result (B) Spin I = 5/2 system (B.1) -3Q antiecho (1) 12-phase cycling the first and the receiver (2) Simulation (3) Result (B.2) +3Q echo (1) 12-phase cycling the first and the receiver (2) Simulation (3) Result (B.3) -5Q echo (1) 20-phase cycling the first and the receiver (2) Simulation (3) Result (B.4) +5Q antiecho (1) 20-phase cycling the first and the receiver (2) Simulation (3) Result (C) Conclusion |
For spin I = 3/2 and 5/2 systems, 12 phases are applied to the first pulse in echo/antiecho acquisition of SPAM MQMAS.
(A) Spin I = 3/2 system
(A.1) -3Q echo
(1) 12-phase cycling the first and the receiver
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | 180° |
| φrec | {0° 270° 180° 90°}X3 |
This 12-phase cycling selects not only the desired coherence transfer pathways
0Q -> -3Q -> (+1Q, 0Q, -1Q) -> -1Q,
but also the coherence transfer pathways
0Q -> -3Q -> (+3Q, +2Q, -2Q, -3Q) -> -1Q,
as shown in the following figure:
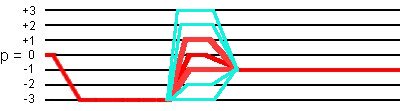
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (-3Q after the first pulse, and +3Q, +2Q,
+1Q, 0Q, -1Q, -2Q, and -3Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 12-phase cycling |
|---|---|---|
| 1st-pulse | na-echo-filt-p1 | na-echo-cycl-p1 |
| 2nd-pulse | na-echo-filt-p2 | na-echo-cycl-p2 |
| 3rd-pulse | na-echo-filt-p3 | na-echo-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 12-phase cycling the first and the receiver) provide the same simulation data for echo amplitude of I = 3/2 system.
(A.2) +3Q antiecho
(1) 12-phase cycling the first and the receiver
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | 0° |
| φrec | {0° 90° 180° 270°}X3 |
This 12-phase cycling selects not only the desired coherence transfer pathways
0Q -> +3Q -> (+1Q, 0Q, -1Q) -> -1Q,
but also the coherence transfer pathways
0Q -> +3Q -> (+3Q, +2Q, -2Q, -3Q) -> -1Q,
as shown in the following figure:
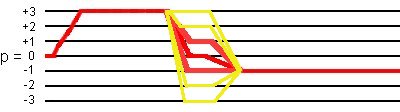
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (+3Q after the first pulse, and +3Q, +2Q,
+1Q, 0Q, -1Q, -2Q, and -3Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 12-phase cycling |
|---|---|---|
| 1st-pulse | na-antiecho-filt-p1 | na-antiecho-cycl-p1 |
| 2nd-pulse | na-antiecho-filt-p2 | na-antiecho-cycl-p2 |
| 3rd-pulse | na-antiecho-filt-p3 | na-antiecho-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 12-phase cycling the first and the receiver) provide the same simulation data for antiecho amplitude of I = 3/2 system.
(B) Spin I = 5/2 system
(B.1) -3Q antiecho
(1) 12-phase cycling the first and the receiver
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | 180° |
| φrec | {0° 270° 180° 90°}X3 |
This 12-phase cycling selects not only the desired coherence transfer pathways
0Q -> -3Q -> (+1Q, 0Q, -1Q) -> -1Q,
but also the coherence transfer pathways
0Q -> -3Q -> (+5Q, +4Q, +3Q, +2Q, -2Q, -3Q, -4Q, -5Q) -> -1Q,
as shown in the following figure:
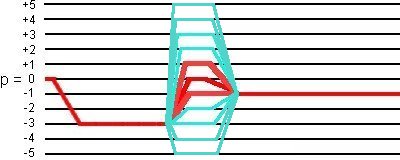
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the antiecho
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (-3Q after the first pulse, and +5Q, +4Q, +3Q, +2Q,
+1Q, 0Q, -1Q, -2Q, -3Q, -4Q, and -5Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 12-phase cycling |
|---|---|---|
| 1st-pulse | al-anti_-3Q-filt-p1 | al-anti_-3Q-cycl-p1 |
| 2nd-pulse | al-anti_-3Q-filt-p2 | al-anti_-3Q-cycl-p2 |
| 3rd-pulse | al-anti_-3Q-filt-p3 | al-anti_-3Q-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 12-phase cycling the first and the receiver) provide the same simulation data for -3Q antiecho amplitude of I = 5/2 system.
(B.2) +3Q echo
(1) 12-phase cycling the first and the receiver
| φ1 | 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° |
|---|---|
| φ2 | 0° |
| φ3 | 0° |
| φrec | {0° 90° 180° 270°}X3 |
This 12-phase cycling selects not only the desired coherence transfer pathways
0Q -> +3Q -> (+1Q, 0Q, -1Q) -> -1Q,
but also the coherence transfer pathways
0Q -> +3Q -> (+5Q, +4Q, +3Q, +2Q, -2Q, -3Q, -4Q, -5Q) -> -1Q,
as shown in the following figure:
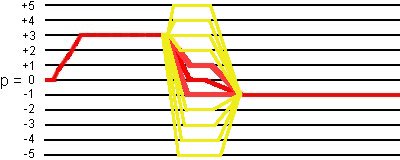
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (-3Q after the first pulse, and +5Q, +4Q, +3Q, +2Q,
+1Q, 0Q, -1Q, -2Q, -3Q, -4Q, and -5Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 12-phase cycling |
|---|---|---|
| 1st-pulse | al-echo-3Q-filt-p1 | al-echo-3Q-cycl-p1 |
| 2nd-pulse | al-echo-3Q-filt-p2 | al-echo-3Q-cycl-p2 |
| 3rd-pulse | al-echo-3Q-filt-p3 | al-echo-3Q-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 12-phase cycling the first and the receiver) provide the same simulation data for +3Q echo amplitude of I = 5/2 system.
(B.3) -5Q echo
(1) 20-phase cycling the first and the receiver
| φ1 | 0° 18° 36° 54° 72° 90° 108° 126° 144° 162° 180° 198° 216° 234° 252° 270° 288° 306° 324° 342° |
|---|---|
| φ2 | 0° |
| φ3 | 180° |
| φrec | {0° 90° 180° 270°}X5 |
This 20-phase cycling selects not only the desired coherence transfer pathways
0Q -> -5Q -> (+1Q, 0Q, -1Q) -> -1Q,
but also the coherence transfer pathways
0Q -> -5Q -> (+5Q, +4Q, +3Q, +2Q, -2Q, -3Q, -4Q, -5Q) -> -1Q,
as shown in the following figure:
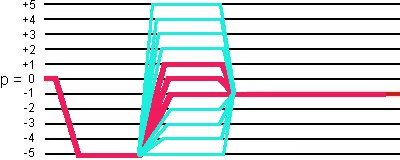
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (-5Q after the first pulse, and +5Q, +4Q, +3Q, +2Q,
+1Q, 0Q, -1Q, -2Q, -3Q, -4Q, and -5Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 20-phase cycling |
|---|---|---|
| 1st-pulse | al_-5Qecho-filt-p1 | al_-5Qecho-cycl-p1 |
| 2nd-pulse | al_-5Qecho-filt-p2 | al_-5Qecho-cycl-p2 |
| 3rd-pulse | al_-5Qecho-filt-p3 | al_-5Qecho-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 20-phase cycling the first and the receiver) provide the same simulation data for -5Q echo amplitude of I = 5/2 system.
(B.4) +5Q antiecho
(1) 20-phase cycling the first and the receiver
| φ1 | 0° 18° 36° 54° 72° 90° 108° 126° 144° 162° 180° 198° 216° 234° 252° 270° 288° 306° 324° 342° |
|---|---|
| φ2 | 0° |
| φ3 | 0° |
| φrec | {0° 270° 180° 90°}X5 |
This 20-phase cycling selects not only the desired coherence transfer pathways
0Q -> +5Q -> (+1Q, 0Q, -1Q) -> -1Q,
but also the coherence transfer pathways
0Q -> +5Q -> (+5Q, +4Q, +3Q, +2Q, -2Q, -3Q, -4Q, -5Q) -> -1Q,
as shown in the following figure:
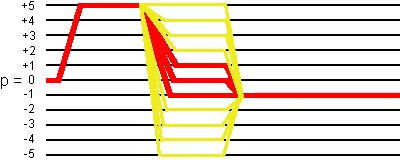
(2) Simulation
We provide SIMPSON1.1.1 Tcl scripts for simulating the echo
amplitude versus a pulse duration with two approaches:
(a) filtering the coherences (+5Q after the first pulse, and +5Q, +4Q, +3Q, +2Q,
+1Q, 0Q, -1Q, -2Q, -3Q, -4Q, and -5Q after the second pulse);
(b) explicit phase cycling the pulses and the receiver.
| Duration | Filtering | 20-phase cycling |
|---|---|---|
| 1st-pulse | al-5Qanti-filt-p1 | al-5Qanti-cycl-p1 |
| 2nd-pulse | al-5Qanti-filt-p2 | al-5Qanti-cycl-p2 |
| 3rd-pulse | al-5Qanti-filt-p3 | al-5Qanti-cycl-p3 |
(3) Result
When the amplitudes are normalized to the number of phase cycling, the two approaches (filtering the coherences and 20-phase cycling the first and the receiver) provide the same simulation data for +5Q antiecho amplitude of I = 5/2 system.
(C) Conclusion
Several SIMPSON1.1.1 Tcl scripts are provided for simulating echo or antiecho amplitudes versus a pulse duration in SPAM MQMAS sequences. Now we can check if the three pulse durations associated with the maximum echo or antiecho amplitudes are identical to those obtained in z-filter MQMAS sequences.
