References for one-pulse nutation NMR

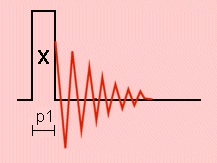
The one-pulse sequence is the simplest NMR experiment. The corresponding one-dimensional nutation method allows us to determine, from a featureless NMR lineshape, the quadrupole coupling in a single crystal or the quadrupole coupling constant in a powder sample.

References containing data and graphs that can be simulated with the one-pulse applets are provided:

1. T. Azaïs, C. Bonhomme, L. Bonhomme-Coury, J. Vaissermann, Y. Millot, P. P. Man, P. Bertani, J. Hirschinger, and J. Livage
   Cubane shaped clusters, precursors for aluminophosphate frameworks: a solid state multinuclear NMR study, in time and frequency domains (PDF article, 337 Kb),
   J. Chem. Soc., Dalton Trans. 609-618 (2002).
2. P. P. Man
   Quadrupole couplings in nuclear magnetic resonance, general (PDF article, 720 Kb),
   in "Encyclopedia of analytical chemistry", edited by R. A. Meyers (J. Wiley, Chichester, 12224-12265, 2000).
3. M. E. Smith and E. R. H. van Eck
   Recent advances in experimental solid state NMR methodology for half-integer spin quadrupolar nuclei,
   Progr. NMR Spectrosc. 34, 159-201 (1999).
4. H. W. Shin, S. H. Choh, T. H. Yeom, K. S. Hong, and D. Y. Han
   1D nutation NMR of ⁷Li in LiTaO₃ and LiNbO₃ single crystals and powders,
   J. Korean Phys. Soc. 32, S662-S664 (1998).
5. A. P. M. Kentgens
   A practical guide to solid-state NMR of half-integer quadrupolar nuclei with some applications to disordered systems,
   Geoderma 80, 271-306 (1997).
6. P. P. Man, S. H. Choh, and J. Fraissard
   Application of 1D nutation NMR to ⁵¹V in ferroelastic BiVO₄,
   Solid State Nucl. Magn. Reson. 3, 231-236 (1994).
7. P. P. Man and P. Tougne
   Exact expression for the spin-7/2 line intensities: application to solid state ⁵⁹Co(III) NMR (PDF article, 499 Kb),
   Mol. Phys. 83, 997-1009 (1994).
8. M. A. Hepp, P. P. Man, A. Trokiner, and J. Fraissard
   Determination of the quadrupole coupling from featureless line shapes,
   Magn. Reson. Chem. 32, 24-28 (1994).
9. P. P. Man
   Excitation conditions for quantitative determination of quadrupolar spins with one-pulse and spin-echo sequences in solid-state NMR,
   Appl. Magn. Reson. 4, 65-87 (1993).
10. P. P. Man
    Analytical expression for the spin-5/2 line intensities,
    Mol. Phys. 78, 307-318 (1993).
11. D. Freude and J. Haase
    Quadrupole effects in solid-state nuclear magnetic resonance,
    in "NMR Basic Principles and Progress", vol. 29, 1-90 (1993).
12. M. A. Hepp, P. P. Man, A. Trokiner, H. Zanni, and J. Fraissard
    Determination of the electric field gradient in RbCaF₃ near the phase transition (PDF article, 397 Kb),
    Solid State Commun. 84, 869-873 (1992).
13. P. P. Man
    Measurement of quadrupolar spin population by solid-state NMR (PDF article, 349 Kb),
    J. Magn. Reson. 77, 148-154 (1988).
14. P. P. Man
    Investigation of the central line of ⁵⁵Mn in KMnO₄ by a two-dimensional NMR method (PDF article, 664 Kb),
    J. Magn. Reson. 67, 78-90 (1986).
15. D. Fenzke, D. Freude, T. Frolich, and J. Haase
    NMR line intensity measurements of half-integer quadrupole nuclei,
    Chem. Phys. Lett. 111, 171-175 (1984).
16. A. Samoson and E. Lippmaa
    Excitation phenomena and line intensities in high-resolution NMR powder spectra of half-integer quadrupolar nuclei,
    Phys. Rev. B 28, 6567-6570 (1983).

SIMPSON scripts and Mathematica-5 notebooks

Use Wolfram CDF Player to read Mathematica notebook in modern web browser.

1. Effet of offset on one pulse 90°(X)-detection applied to positive gyromagnetic ratio nucleus:
   *magnetization x component,
   *magnetization y component,
   *magnetization z component,
   *corresponding Mathematica 5 notebook.
2. Effet of offset on one pulse 90°(-X)-detection applied to positive gyromagnetic ratio nucleus:
   *magnetization x component,
   *magnetization y component,
   *magnetization z component,
   *corresponding Mathematica 5 notebook.
3. Effet of offset on one pulse 90°(Y)-detection applied to positive gyromagnetic ratio nucleus:
   *magnetization x component,
   *magnetization y component,
   *magnetization z component,
   *corresponding Mathematica 5 notebook.
4. Composite rotation matrices in Mathematica-5 notebook:
   *passive rotation about rotated coordinate axes,
   *active rotation about rotated coordinate axes.