We have simulated the same experiment as that described in Example 1 using SIMPSON version 1.1.0, a general simulation program for solid-state NMR spectroscopy provided by M. Bak, J. T. Rasmussen, and N. C. Nielsen, J. Magn. Reson. 147, 296-330 (2000).

# twop1.in
# spin-3/2 central-line intensity optimization
# with p1 in two-pulse MAS sequence

spinsys {
  channels 23Na
  nuclei   23Na
  quadrupole 1 1 1e6 0 0 0 0
}



par {
  spin_rate        10000
  variable tsw     0.5
  sw               1.0e6/tsw
  np               41
  crystal_file     rep320
  gamma_angles     10
  start_operator   I1z
  verbose          1101
  variable rf      100000
  proton_frequency 400e6
}

proc pulseq {} {
  global par
  maxdt $par(tsw)

  matrix set 1 elements {{1 4} {4 1}}




  matrix set detect elements {{2 3}}



  acq

  for {set i 1} {$i < $par(np)} {incr i} {

    pulse $par(tsw) $par(rf) x


    store 2



    filter 1


    pulse 1.5 $par(rf) x


    acq -y

    reset


    prop 2
  }
}

proc main {} {
  global par

  fsave [fsimpson] $par(name).fid
  puts "Larmor frequency (Hz) of 23Na: "
  puts [resfreq 23Na $par(proton_frequency)]
}
    

File name.
Description.




Spin I = 3/2.
1st-order
quadrupole
interaction,
qcc = 1 MHz,
eta = 0.

10 kHz.
0.5 µs increment.

1st pulse: 20 µs.




100 kHz RF pulse.





0.5 µs increment.

3Q and -3Q from
the 1st pulse,
density matrix
convention.

Central transition,
fictitious spin-1/2
convention.

No pulse,
no signal.


1st x-pulse is
variable pulse.

Save propagator
at the end of 
1st x-pulse.

Select -3Q and 3Q
coherences.

The 2nd x-pulse
has 1.5 µs duration.

Receiver -y.

Reset propagator to
initial value.

Recall the propagator
at the end of the
1st x-pulse.
      

SIMPSON uses gyromagnetic ratios provided by IUPAC for the determination of the Larmor frequency of a nucleus. For example:

²³Na Larmor frequency = Proton Larmor frequency * ²³Na gyromagnetic ratio / Proton gyromagnetic ratio;

400 MHz * 7.0808493 / 26.7522128 = 105.8731007 MHz.

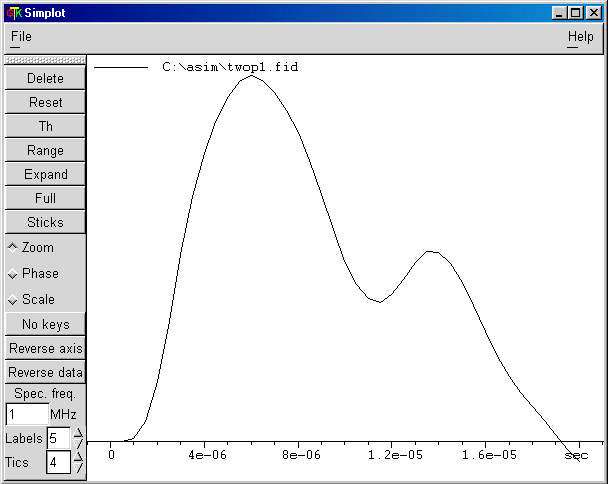
This curve represents the simulated central-line intensity versus the first-pulse length p1 with SIMPSON for a spin I = 3/2 system excited by the two-pulse MAS sequence.

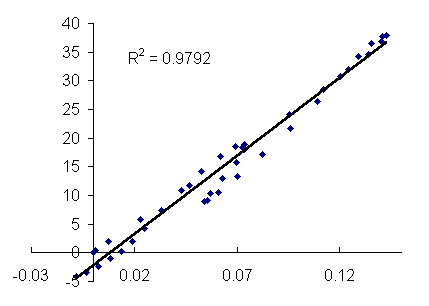
This figure represents the correlation curve relating two simulations generated with SIMPSON (Simpson 1) and JDK1.3 Java applet (Example 1) for the two-pulse MAS sequence applied to a spin I = 3/2 system.