Analytical expression of V(2,0) for static crystal in NMR
The first-order quadrupole interaction is related to V(2,0):
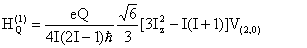
In static NMR experiment, V(2,0) is defined by:
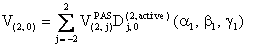
Its analytical expression can be determined as follows:
(1) Select and copy the following green lines; then paste them into a cell of Mathematica, a software for numerical and symbolic calculations.
(2) Press "Ctrl-A" for select all; then
press "Shift-enter" for evaluate cells.
(Or in the menu bar, select Kernel > Evaluation > Evaluate Cells)
Using Mathematica-5 running with a 3-GHz processor, the analytical expression of V(2,0) is obtained in 5 seconds.
(* V2pas is a row-matrix with 3 columns
containing the 3 nonzero eigenvalues of the EFG
expressed as a 2-nd rang spherical tensor, in eq unit *)
V2pas = {{eta/2, Sqrt[3/2], eta/2}};
(* D2 is a reduced form (3 rows x 1 column) of the 2-nd order
Wigner active rotation matrix *)
D2 = {
{Sqrt[3/8]*Sin[beta1]^2*E^(-2*I*alpha1)},
{(-1 + 3*Cos[beta1]^2)/2},
{Sqrt[3/8]*Sin[beta1]^2*E^(2*I*alpha1)}
};
(* V20static is an expression *)
V20static = FullSimplify[V2pas.ComplexExpand[D2]];
(* suppression of the double curve brackets {{}} of V20static *)
Print[V20static[[1, 1]]];
Remove[V2pas, eta, D2, alpha1, beta1, V20static];
