Definition of cogwheel phase cycling parameters

1. Introduction

In 2002, Levitt and coworkers introduced the cogwheel phase cycling in NMR to reduce the number of steps for coherence transfer pathway selection. The various parameters involved in this approach require a numerical search. We present a procedure using XML (eXtensible Markup Language) for modelling the pulse sequence with cogwheel phase cycling and XSLT (eXtensible Stylesheet Language Transformation) for numerical search of these parameters.

2. Split-t1 MQMAS sequence

We illustrate our web-tool approach with the well-studied sequence: the selection of the antiecho coherence transfer pathway in a three-pulse split-t1 MQMAS sequence applied to a spin I = 3/2 system.

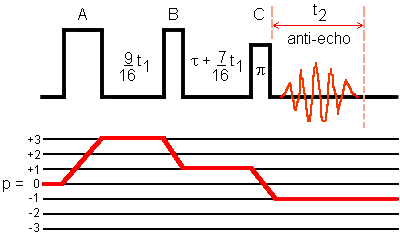
In cogwheel phase cycling, the phases of the three pulses (A, B, and C) are incremented simultaneously as:

where $w_A$, $w_B$, and $w_C$ are integers called winding numbers, N is the number of steps in the phase cycling, and m is the phase counter (N - 1 ≥ m ≥ 0). These definitions are used by Levitt and coworkers.

The signal S(p) from a general coherence transfer pathway p = {0Q -> $p_{\mathrm{AB}}$Q -> $p_{\mathrm{BC}}$Q -> -1Q} is given by:

The desired coherence transfer pathway is $p^0$ = {0Q -> $p_{\mathrm{AB}}^0$Q -> $p_{\mathrm{BC}}^0$Q -> -1Q}. That is, $p_{\mathrm{AB}}^0$ = 3 and $p_{\mathrm{BC}}^0$ = 1 for this MQMAS sequence.

The signal S(p) is not zero if the following condition is fulfilled:

The main difficulty about the cogwheel phase cycling is the numerical search about the number of steps N and the winding numbers. Fortunately, several rules have been established by Levitt and coworkers in 2004.