Second-order quadrupole shift for MAS rotating crystal
The second-order quadrupole interaction is related to V(2,±1) and V(2,±2):
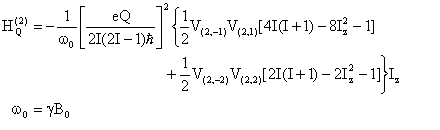
(Eq. 1)
The second-order quadrupole interaction shifts the energy level |m> by an amount:
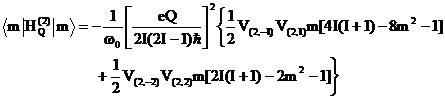
(Eq. 2)
In the spectrum, the second-order quadrupole shift of the line position associated with the transition (m - 1, m) is
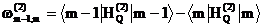
(Eq. 3a)
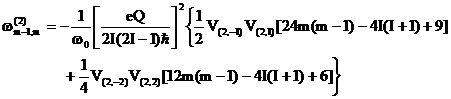
(Eq. 3b)
In MAS NMR experiment, V(2,p) is defined by
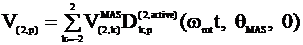
(Eq. 4)
and V(2,k)MAS by
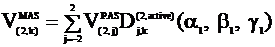
(Eq. 5)
For MAS rotating crystal, first Eq. 4 is used in Eq. 3b. The second-order quadrupole shift of the central-transition line with m = 1/2 is
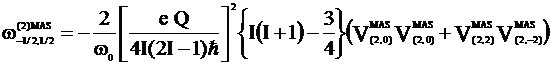
(Eq. 6)
Then Eq. 5 is used in Eq. 6 that becomes:
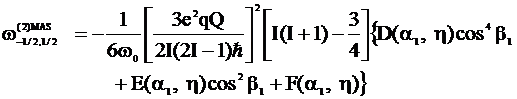
(Eq. 7)
with
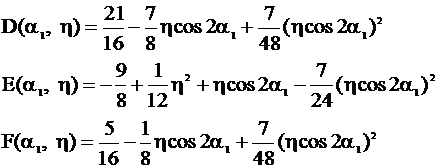
(Eq. 8)
We also provide Mathematica notebook for calculating V(2,1)V(2,-1) and V(2,2)V(2,-2) in the condition of fast rotating crystal. They allow us to define Eq. 6. This notebook also generate V(2,2)MASV(2,-2)MAS + (V(2,0)MAS)2 used in Eq. 6. Their analytical expressions can be determined as follows:
(1) Select and copy the following green lines; then paste them into a cell of Mathematica, a software for numerical and symbolic calculations.
(2) Press "Ctrl-A" for select all; then
press "Shift-enter" for evaluate cells.
(Or in the menu bar, select Kernel > Evaluation > Evaluate Cells)
Using Mathematica-5 running with a 3-GHz processor, these analytical expressions are obtained in 13 seconds.
(*The EFG tensor in the reference MAS, V2kMAS is a row - matrix with 5 columns*)
V2kMAS = {V22MAS, V21MAS, V20MAS, V2m1MAS, V2m2MAS};
(*D21MAS and D2m1MAS are reduced forms (5 rows x 1 column) of the 2-nd
order Wigner active rotation matrix*)
D21MAS = {{-(1/2)(1 + Cos[thetaMAS])Sin[thetaMAS]*E^(-2I rot*t)},
{(Cos[thetaMAS]^2 - (1/2)(1 - Cos[thetaMAS]))*E^(-I rot*t)},
{Sqrt[3/8]Sin[2thetaMAS]},
{( (1/2)(1 + Cos[thetaMAS]) - Cos[thetaMAS]^2)*E^(I rot*t)},
{(1/2)(1 - Cos[thetaMAS])Sin[thetaMAS]*E^(2I rot*t)}};
D2m1MAS = {{-(1/2)(1 - Cos[thetaMAS])Sin[thetaMAS]*E^(-2I rot*t)},
{((1/2)(1 + Cos[thetaMAS]) - Cos[thetaMAS]^2)*E^(-I rot*t)},
{-Sqrt[3/8]Sin[2thetaMAS]},
{(Cos[thetaMAS]^2 - (1/2)(1 - Cos[thetaMAS]))*E^(I rot*t)},
{(1/2)(1 + Cos[thetaMAS])Sin[thetaMAS]*E^(2I rot*t)}};
(*D22MAS and D2m2MAS are reduced forms (5 rows x 1 column)
of the 2-nd order Wigner active rotation matrix*)
D22MAS = {{(1/4)(1 + Cos[thetaMAS])^2*E^(-2I rot*t)},
{(1/2)(1 + Cos[thetaMAS])Sin[thetaMAS]*E^(-I rot*t)},
{Sqrt[3/8]Sin[thetaMAS]^2},
{(1/2)(1 - Cos[thetaMAS])Sin[thetaMAS]*E^(I rot*t)},
{(1/4)(1 - Cos[thetaMAS])^2*E^(2I rot*t)}};
D2m2MAS = {{(1/4)(1 - Cos[thetaMAS])^2*E^(-2I rot*t)},
{-(1/2)(1 - Cos[thetaMAS])Sin[thetaMAS]*E^(-I rot*t)},
{Sqrt[3/8]Sin[thetaMAS]^2},
{-(1/2)(1 + Cos[thetaMAS])Sin[thetaMAS]*E^(I rot*t)},
{(1/4)(1 + Cos[thetaMAS])^2*E^(2I rot*t)}};
(*thetaMAS is the magic angle*)
D21MAS = D21MAS /. {thetaMAS -> ArcCos[Sqrt[1/3]]};
D2m1MAS = D2m1MAS /. {thetaMAS -> ArcCos[Sqrt[1/3]]};
D22MAS = D22MAS /. {thetaMAS -> ArcCos[Sqrt[1/3]]};
D2m2MAS = D2m2MAS /. {thetaMAS -> ArcCos[Sqrt[1/3]]};
(*V21mas, V2m1mas, V22mas, and V2m2mas are expressions*)
V21mas = FullSimplify[ComplexExpand[V2kMAS.ComplexExpand[D21MAS]]];
V2m1mas = FullSimplify[ComplexExpand[V2kMAS.ComplexExpand[D2m1MAS]]];
V22mas = FullSimplify[V2kMAS.ComplexExpand[D22MAS]];
V2m2mas = FullSimplify[V2kMAS.ComplexExpand[D2m2MAS]];
z21mas = Expand[V21mas*V2m1mas] ;
z22mas = Expand[V22mas*V2m2mas] ;
(*In rapid rotation of the sample*)
z21mas = z21mas /. {E^(x_) -> 0};
z22mas = z22mas /. {E^(x_) -> 0};
Vterm = FullSimplify[z21mas(24m(m - 1) - 4S(S + 1) + 9) + (1/2)z22mas (12m(
m - 1) - 4S(S + 1) + 6)];
VtermMAS = Collect[Collect[Collect[Vterm,
V20MAS^2], V21MAS V2m1MAS], V22MAS V2m2MAS];
VtermMAS = FullSimplify[
Expand[VtermMAS[[1, 1]]]] + FullSimplify[Expand[VtermMAS[[1,
2]]]] + FullSimplify[Expand[VtermMAS[[1, 3]]]];
VtermMAS = VtermMAS /. {m -> 1/2};
VtermMAS = Simplify[VtermMAS];
coef1 = "omega(2)MAS(-1/2,1/2) = (-2/omegaLarmor)(eQ/(4S(2S-1)hBar))^2 {";
Print[coef1, VtermMAS, "}"];
(**************************************************************************)
(*In the reference PAS, V2pas is a row - matrix with 3 columns containing the
3 nonzero eigenvalues of the EFG expressed as a 2-nd rang spherical tensor,
in eq unit*)
V2pas = {{eta/2, Sqrt[3/2], eta/2}};
(*D2 is a reduced form (3 rows x 1 column) of the 2 - nd order Wigner active
rotation matrix*)
D20 = {{Sqrt[3/8]*Sin[beta1]^2*E^(-2I alpha1)},
{(-1 + 3*Cos[beta1]^2)/2},
{Sqrt[3/8]*Sin[beta1]^2*E^(2I alpha1)}};
(*V20MAS is an expression*)
V20MAS = FullSimplify[V2pas.ComplexExpand[D20]];
V0MAS = Expand[V20MAS*V20MAS];
(*************************************************)
(*D22 and D2m2 are reduced forms (3 rows x 1 column) of the 2-nd order
Wigner active rotation matrix*)
D22 = {{(1/4)(1 + Cos[beta1])^2*E^(-2I(alpha1 + gamma1))},
{Sqrt[3/8]Sin[beta1]^2*E^(-2I gamma1)},
{(1/4)(1 - Cos[beta1])^2*E^(2I(alpha1 - gamma1))}};
D2m2 = {{(1/4)(1 - Cos[beta1])^2*E^(-2I(alpha1 - gamma1))},
{Sqrt[3/8]Sin[beta1]^2*E^(2I gamma1)},
{(1/4)(1 + Cos[beta1])^2*E^(2I(alpha1 + gamma1))}};
(*V22MAS and V2m2MAS are expressions in eq units*)
V22MAS = FullSimplify[V2pas.ComplexExpand[D22]];
V2m2MAS = FullSimplify[V2pas.ComplexExpand[D2m2]];
(*V2MAS is an expression in eq.eq units*)
V2MAS = TrigExpand[V22MAS V2m2MAS];
(*************************************************)
Vterm = V2MAS + V0MAS;
Vterm = Expand[Vterm /. {Sin[beta1]^2 -> 1 - Cos[beta1]^2,
Sin[beta1]^4 -> 1 - 2 Cos[beta1]^2 + Cos[beta1]^4,
Sin[alpha1]^4 -> 1 - 2 Cos[alpha1]^2 + Cos[alpha1]^4,
Sin[2alpha1]^2 -> 1 - Cos[2alpha1]^2,
Sin[alpha1]^2 -> 1 - Cos[alpha1]^2}];
Vterm = Expand[Vterm /. {Cos[alpha1]^2 -> (1 + Cos[2alpha1])/2,
Cos[alpha1]^4 -> (1 + Cos[2alpha1])^2/4}];
Vterm = Collect[Collect[Vterm, Cos[beta1]^4], Cos[beta1]^2];
(*Suppression of the double curve brackets {{}} of Vterm*)
ome = Vterm[[1, 1]];
long = Length[ome];
Vterm = Factor[Take[ome, long -
2]] + Factor[ome[[long - 1]]] + Factor[ome[[long]]];
coef2 = "omega(2)MAS(-1/2,1/2) = (-2/omegaLarmor)(eQeq/(4S(2S-1)hBar))^2 ((-3/4)+(S+1)S){";
Print[coef2, Vterm, "}"];
Remove[D21MAS, D2m1MAS, D22MAS, D2m2MAS, V2kMAS, V21mas, V2m1mas, V22mas,
V2m2mas, z21mas, z22mas, ome, V2pas, D20, D22, D2m2, V22MAS,
V2m2MAS, V20MAS, V2MAS, V0MAS, VtermMAS, Vterm, coef1, coef2];
