Why one of the rf pulses in a multiple-pulse sequence does not need to be phase cycled?

Consider a three-pulse sequence for simplicity. It is easy to show that Pulse-3 does not need to be phase cycled, for example.

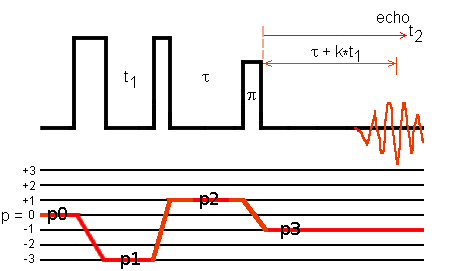
The receiver phase φ_rec is defined by
φ_rec = -φ1*Δp1 - φ2*Δp2 - φ3*Δp3, (Eq. 1)
where φi is the phase of Pulse-i and Δpi is the difference between the coherence order p after Pulse-i and that before Pulse-i. That is
Δp1 = p1 - p0, Δp2 = p2 - p1, and Δp3 = p3 - p2
where p0 = 0 and p3 = -1.

Since Δp1 + Δp2 + Δp3 = -1 whatever the coherence transfer pathway is, we replace Δp3 in the expression of the receiver phase (Eq. 1) by
Δp3 = -1 - Δp1 - Δp2.
As a result, the expression of the receiver phase becomes
φ_rec - φ3 = -(φ1 - φ3)*Δp1 - (φ2 - φ3)*Δp2, (Eq. 2)
which can be rewritten as
ψ_rec = -ψ1*Δp1 - ψ2*Δp2.
The phase of Pulse-3 does not appear in the definition of the receiver phase.

This result is in agreement with the well-known property in phase cycling:
"additing a constant phase to the receiver phase and to those of all the rf pulses does not change the NMR signal".

Application of this property to Eq. 1 gives Eq. 2.