Definition of echo and antiecho signals in MQMAS NMR
Definition of echo and antiecho signals in MQMAS NMR
In ±3QMAS NMR of a spin I = 5/2 system, an echo signal E(t1, t2) and an antiecho signal A(t1, t2) have the following expressions:
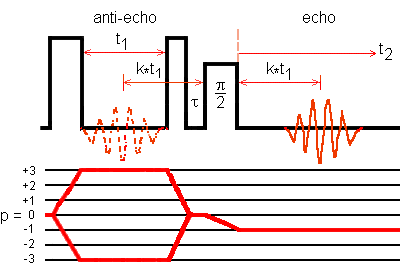
Fig. 1: Z-filter 3QMAS NMR pulse sequence and coherence transfer pathway.
The echo amplitude and the antiecho amplitude have the
same sign.
The three-pulse z-filter MQMAS sequence generates echo and antiecho, which have the same amplitude with the same sign.
The detected signal is the contribution of E(t1, t2) and A(t1, t2):
S3(t1, t2) = H.E(t1, t2) + H.A(t1, t2)
The amplitude H is a complex number. The 2D Fourier transform of S3(t1, t2) generates phase-twisted 2D peak.
The standard solution to this problem is the application of States procedure to generate 2D pure absorption peak. It consists in acquiring two complementary signals:
The echo SE(t1, t2) and antiecho SA(t1, t2) signals are obtained from Sx(t1, t2) and Sy(t1, t2):
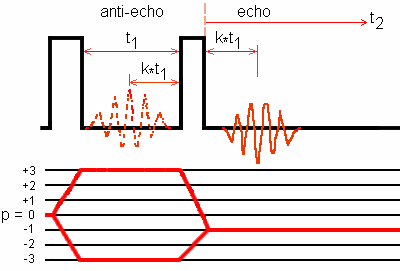
Fig. 2: Amplitude-modulated two-pulse 3QMAS NMR pulse sequence and coherence
transfer pathway.
The echo amplitude and the antiecho amplitude have
opposite signs.
The two-pulse MQMAS sequence generates echo and antiecho, which do not have the same amplitude but with opposite signs.
The detected signal is the contribution of E(t1, t2) and A(t1, t2):
S2(t1, t2) = H.E(t1, t2) - H.A(t1, t2)
For simplicity, they are supposed to have opposite amplitudes. The 2D Fourier transform of S2(t1, t2) generates phase-twisted 2D peak.
The States procedure consists in acquiring two complementary signals:
The echo SE(t1, t2) and antiecho SA(t1, t2) signals are obtained from Sx(t1, t2) and Sy(t1, t2):
For these two pulse sequences in ±3QMAS NMR of a spin I = 5/2 system, the echo SE(t1, t2) and antiecho SA(t1, t2) signals are obtained with the same formulas:
These two formulas are a consequence of the +π/2 angles involved in Sy(t1, t2). This +π/2 angle is included in the pulse program by applying to the first pulse a phase change of +π/|2p| for Sy(t1, t2) acquisition.
Conversely, Sx(t1, t2) and Sy(t1, t2) can be expressed as:
In the States method, pure 2D absorption spectrum is the Fourier transform in
the t1 domain of
Re[Sx(t1, ω2)] + i.Re[Sy(t1, ω2)]