Example 2 of two-pulse MAS simulation

The example, which is complementary to Example 1, also deals with the central-line intensity of a spin I = 3/2 in a powder sample rotating at the magic angle with a rotor speed of 10 kHz.

The strength of the RF magnetic field is 100 kHz.

The values of the two quadrupole parameters are 1000 kHz for the quadrupole coupling constant QCC and 0 for the asymmetry parameter eta.

The simulation associated with the two-pulse sequence is A()B(p2), where the second-pulse length p2 increases from 0 to 10 µs by 0.25 µs step; the first-pulse length p1 is 6 µs. There is no interpulse delay (tau1 = 0, this is an approximation) whereas experimental tau1 is about 10 µs.

The pulse length to pulse increment ratios are integers.

The number of integration steps for alpha and for beta Euler angles are MaxAlpha = 20, that for gamma Euler angle is MaxGamma = 10.

The first pulse excites the ±3-quantum coherences simultaneously.

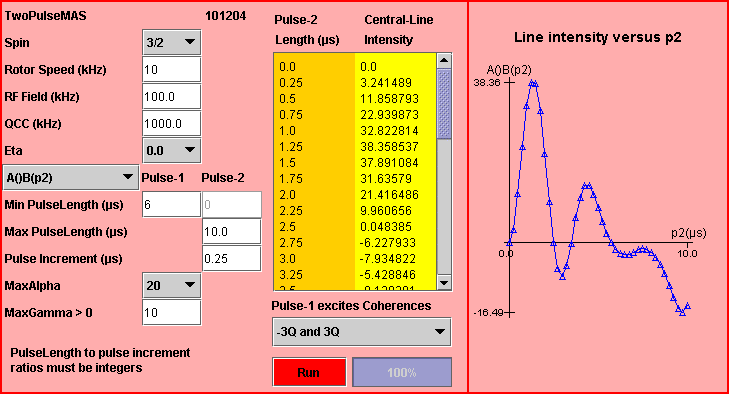
The sign of the central-line intensity changes several times for a range of the second-pulse length p2 that is much shorter than that of the first-pulse length p1 in Example 1.